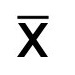Median, a common measure of central tendency and averages, is the numerical value separating the higher half and lower half of a data set. Median calculation is used in multiple branches of mathematics but it is primarily used in probability and statistics.
To calculate the median of a data set, you first must start by ordering the data set in numerical order. After the values are ordered, you simply take the middle number of the data as your median. If no true middle value exists, you must add the middle two values and divide by 2.

For a simple example, let’s pretend we have sample data of the number of absences of the 3 students in your math class. The data set over the course of a year is as follows: [6,2,3]. First, start by rearranging the data in numerical order which produces the following: [2,3,6]. Next, to find the median we simply find the middle value of the sample. The median of this data set is 3 as it is the true middle between 2 and 6.

When your data set contains an odd amount of values such as above, your median will always be one of the values from the data set. However, if your data set contains an even amount of values, you can end up with a median which doesn’t match any particular value in the data set.

For a more complicated example, let’s pretend we have sample data of the number of absences of the 6 students in your science class. The data set over the course of a year is as follows: [2,4,5,1,6,0]. Once again, begin by numerically ordering the sample data which results in the following: [0,1,2,4,5,6]. As there is an even number of values in the data set, there is no true middle value. To complete the median calculation for this data set you must take the middle two values, 2 and 4, and divide their total by 2. In this case, you would take (2+4) / 2, giving you a median value of 3.

To use our median calculator, simply enter your data set with all values separated by commas and no spaces. For example: 2,6,7,1,3. Our calculator will automatically arrange your data set in numerical order.